Numerical Magnetohydrodynamics

Some Initial Remarks

The field of hydrodynamics (HD for short) seeks to describe a liquid's motion in a given environment, as it results from the forces which act upon the fluid. It has been generalized to apply to compressible media (gases), and nowadays has a vast range of application in science and technology, comprising, among other things, oceanography, weather and climate studies, aeronautical engineering, flow studies related to vehicle design, and the like.

In many astrophysical settings (like the Sun's interior, as well as the interplanetary and interstellar medium), the gas is ionized, such that its motion is subject not only to gas pressure and gravity, but also to electromagnetic forces. Their incorporation into the fluid picture of HD results in a set of similar (but somewhat more complicated) equations, which then constitute the extension of HD to magnetohydrodynamics (MHD for short).

The (M)HD approach of treating an assembly of (many) atoms and molecules as a continuous medium critically relies on the assumption that the length and time scales on which any two particles interact (e.g. via collisions) is negligible against the macroscopic scales which are to be considered. But while this is usually well satisfied for air or water, magnetized gases (especially those usually considered in astrophysics) present a more complex issue, and can often exhibit collective behavior of particle ensembles resulting in macroscopic effects of the gas/fluid as a whole. Therefore, the validity of the MHD picture for a given astrophysical setting has to be assessed carefully before it is applied.

Accuracy vs. Simplicity

As with many objects of scientific study, the theoretical investigation of magnetized fluids relies upon models to study their characteristic properties. The delicate task is to choose a model which is complex enough to capture the key characteristics of its real-world counterpart, while at the same time remaining simple enough to be handled and understood. In a hierarchy of increasing complexity, major model approaches developed to study the dynamics of ionized gases can be grouped as follows:

• Single-fluid MHD treats the gas/liquid as a single fluidal component. This approach requires that the system's length scales be much larger than the size of single-particle effects, such as the radius of the spiraling path along which electrons and ions move around magnetic field lines. Analytic solutions are known for many (idealized) situations.
• Multi-fluid MHD retains the notion of continuous fluids but treats electrons, ions, and possibly additional components like dust as individual, co-existing fluids, each of which is characterized by its respective density and temperature distribution and velocity field. Analytic solutions are very sparse.
• Hybrid models still treat electrons as a fluid, whereas the dynamics of all other components are explictly followed as particle trajectories. Practically no analytic solutions from now on.
• Kinetic simulations completely abandon the notion of continuous fluids and directly consider distributions of individual particles for all species (electrons, ions, dust, ...).

The Need for Numerics

The equations of MHD represent a coupled set of partial differential equations in four dimensions of space and time for the scalar and vector quantities like density, velocity, magnetic field, and gas pressure. For some problems, simplifications such as symmetry assumptions, neglect of fluid inertia, or reduced self-consistency can reasonably be made, thus allowing for analytic or semi-analytic solutions. However, the generic case does not allow for such assumptions to be made, and a recourse to numerical approximation becomes mandatory.

The procedure first requires the spatial domain under consideration to be subdivided into (reasonably many) grid cells, inside of which all physical quantities are assumed constant. This of course implies that a trade-off must be found between a precise description of the physics (asking for the cells to be very small), and the need to keep track of the temporal changes of the cells (placing an effective upper limit on the total number of cells, and thus on the minimum cell size). The differential MHD equations are then discretized on this grid, resulting in a large system of difference equations which, when solved, determines the new cell contents at a given time t as a function of their contents at some earlier time t-dt. Starting from some prescribed initial condition, repeated application of this scheme will finally yield the system's state at an arbitrary later time.

It should be noted, however, that the discretization of equations is not at all unique, and each method comes with its own special advantages and shortcomings (including different types of artefacts, spurious deviations from the 'true' solution which may at times be difficult to spot, and even more difficult to reduce to an acceptable level).

Application #1: Single-fluid MHD for Solar Wind Expansion

Collaborators: Horst Fichtner, Andreas Kopp

Application #2: Multi-fluid MHD of SW <-> Planet Interaction

Collaborators: Andreas Kopp, Konrad Sauer

When the solar wind encounters a massive object like a planet or a comet, it is forced to decelerate, causing various so-called plasma boundaries to develop. Most notably among these are the bow shock (at which the flow becomes sub-Alfvenic), and the magnetic pile-up boundary (where the IMF's field lines drape around the obstacle, causing a steep rise in magnetic field strength). The rise of such ion tails is a classic example of a gyration effect (i.e. of the ion gyro-radius being comparably to or even larger than the planet's radius) which is completely unaccessible to standard one-fluid MHD. This example may thus illustrate the importance of a well-chosen model for a given (astro)physical problem. It also shows that the need to capture gyration effects alone does not justify the extra effort of hybrid/kinetic models, since the multi-fluid approach is well capable of describing these effects properly.
The crucial advantage of fully three-dimensional computations becomes particularly evident in the case of asymmetric structures, as illustrated by the figures of Panel 2.

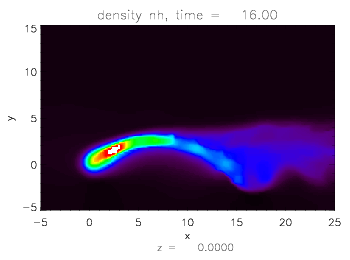
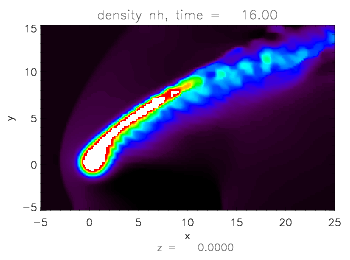
Panel 1: Contour plots of cometary ion density for different values of mass loading rate and cometary ion mass number (left: A=2, right: A=10). The magnetic field is pointing upwards, while the solar wind is incident from the left at twice the Alfven velocity. As mass loading increases, clump-like instabilities arise in the comet's tail. (Click on images to download the respective MPEG movies.)

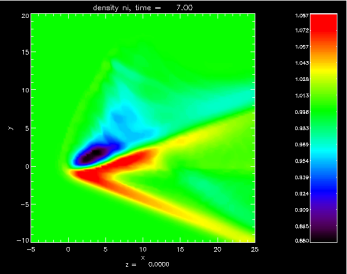
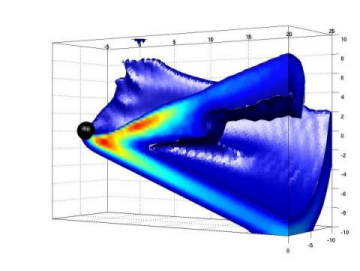
Panel 2: The left figure shows a density contour plot in the plane of incoming flow (from the left) and the magnetic field (initially oriented vertically, not shown here). Asymmetric, cone-like structures emanate from the obstacle, whose shape departs markedly from the cylindrically-symmetric Mach cones known from HD or single-fluid MHD simulations. Using a 3D grid for the simulation, the cone structure can easily be visualized generating rotational iso-surfaces, as shown in the figure to the right. (Click on the left image for a larger view, or the right image for an MPEG movie featuring a full 360° rotation of this configuration.)